C/C++全栈开发学习笔记

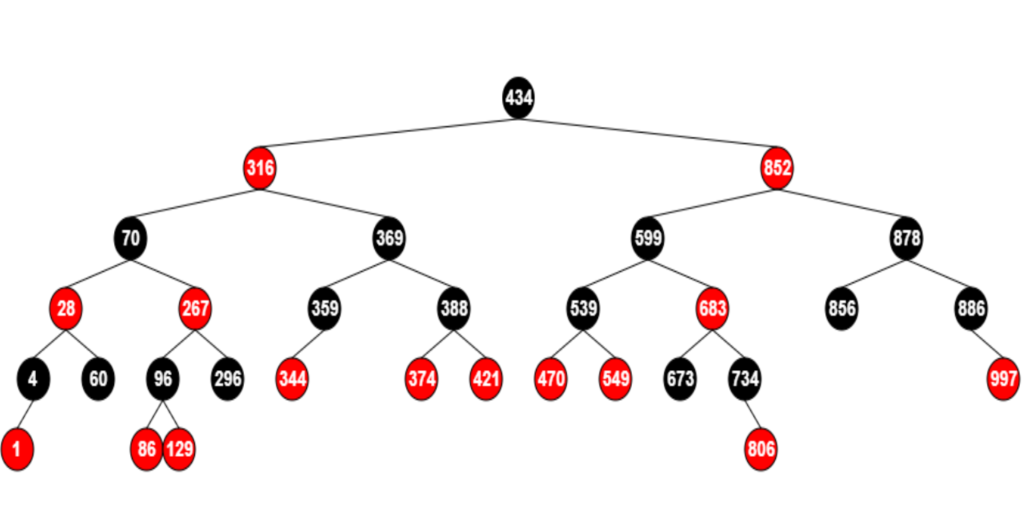
1.1.1 随处可见的红黑树

学习目标：

能使用C语言实现红黑树
能记住红黑树的代码实现

红黑树的性质：

每个结点是红的或者黑的
根结点是黑的
每个叶子结点是黑的
如果一个结点是红的，则它的两个儿子都是黑的（不存在相邻红色）
对每个结点，从该结点到其子孙结点的所有路径包含相同数目的黑节点（即黑高度相同）
最长路径长度不超过最短路径长度的2倍（2n-1，一条黑红黑红，一条全黑）

红黑树的优点：插入和删除的时间复杂度优于平衡二叉搜索树，又没有二叉搜索树可能退化为链表的Bug

rbTree查询元素：O(log(N))
rbTree插入元素：插入最多2次旋转，加上查询的时间O(log(N))，插入的复杂度O(log(N))
rbTree删除元素：删除最多需要3次旋转，加上查询的时间，删除的复杂度O(log(N))

红黑树的应用场景

c++ stl map,set（红黑树的封装）
进程调度cfs（用红黑树存储进程的集合，把调度的时间作为key，那么树的左下角时间就是最小的）
内存管理（每次使用malloc的时候都会分配一块小内存出来，那么这么块就是用红黑树来存，如何表述一段内存块呢，用开始地址+长度来表示，所以key->开始地址，val->大小）
epoll中使用红黑树管理socketfd
nginx中使用红黑树管理定时器，中序遍历第一个就是最小的定时器

红黑树结点的定义

typedef struct _rbtree_node {
    //rbtree
    unsigned char color; // #define RED 0 define BLACK 1
    struct _rbtree_node *parent;
    struct _rbtree_node *left;
    struct _rbtree_node *right;
    

    KEY_TYPE key; // 例如 typedef int KEY_TYPE 

    // value	// value 的类型也是自己定义
    //
} rbtree_node;

红黑树的定义

struct rbtree {
    // 只需要一个 root 根结点
    rbtree_node *root;
    // 红黑树中空结点的类型也是红黑树结点，也有left、right、parent指针
    rbtree_node *nil; // NULL 
};

红黑树的四个难点：删除、插入、调整、左旋右旋

红黑树结点的左旋与右旋

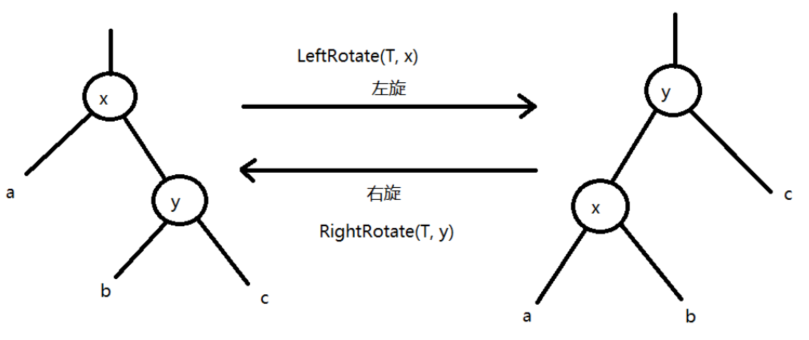
红黑树的左旋操作：左旋就是向左倾斜，记住要操作三条线，六个指针，分别是:

x->right = y->left | y->left->parent = x
y->parent = x->parent | x->parent->left/right = y
x->parent->left/right = y | y->left->parent = x

void rbtree_left_rotate(struct rbtree *T, rbtree_node *x) {
	// 左旋只需要一个结点就能完成，引入 T 是为了判断是否为根结点或者叶子结点
	if(x == T->nil)  return;
	// 直接读取左旋需要的右节点
	rbtree_node *y = x->right;
	// x到y的那条线
	x->right = y->left;
	if(y->left != T->nil) {
		y->left->parent = x;
	}
	// x上面那条线
	y->parent = x->parent;
    if(x->parent == T->nil) {  // 如果x是根节点
        T->root = y;
    } else if(x == x->parent->left) { // 否则判断x是x父节点的左结点还是右节点
    	x->parent->left = y;
    } else {
        x->parent->right = y;
    }
    // y到b那条线
    y->left = x;
    x->parent = y;
}

红黑树的右旋操作：右旋就是向右倾斜，由于左旋和右旋是完全对称的，因此在代码上可以直接替换来实现右旋

// x --> y, y -->x 
// left --> right, right --> left
void rbtree_right_rotate(struct rbtree *T, rbtree_node *y) {
    // NULL --> T->nil
    if (y == T->nil) return ;
    rbtree_node *x = y->left;
	// y到x的那条线
    y->left = x->right;
    if (x->right != T->nil) {
        x->right->parent = y;
    }
    // y上面那条线
    x->parent = y->parent;
    if (y->parent == T->nil) {
        T->root = x;
    } else if (y == y->parent->right) {
        y->parent->right = x;
    } else {
        y->parent->left = x;
    }
    // x到b那条线
    x->right = y;
    y->parent = x;
}

注意红黑树的左旋右旋代码执行顺序

红黑树插入结点后的调整

当插入一个结点时，有时要对红黑树进行调整，包括变色和左旋右旋以及回溯这三个操作

CASE 1：父节点是爷结点的左子树且叔结点是红色的

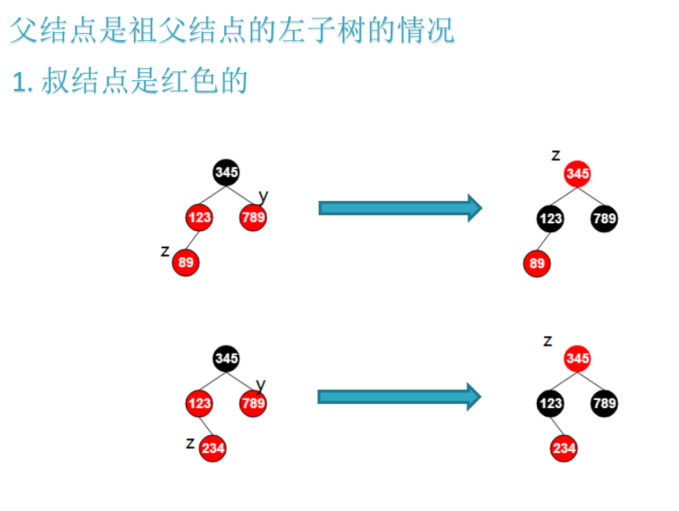
无需旋转，只需要将父节点和叔结点变黑，将爷结点变红，然后令z指向爷结点即回溯调整

CASE 2：父节点是叶结点的左子树的情况且叔结点是红色以及当前结点是右孩子

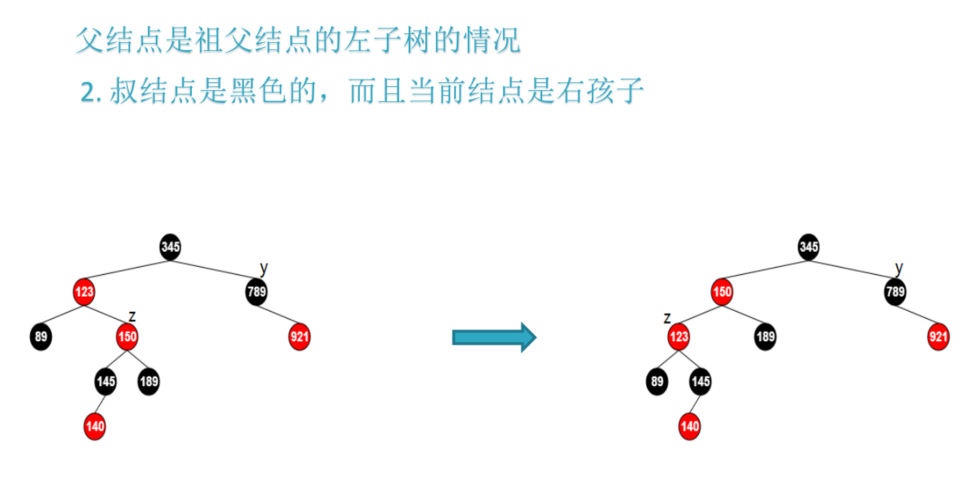
此时需要先旋转变为第三种情况，然后按照第三种情况处理，即让当前结点指向其父结点并进行一次左旋

CASE 3：父节点是祖父结点的左子树且叔节点是黑色的以及当前结点是左孩子

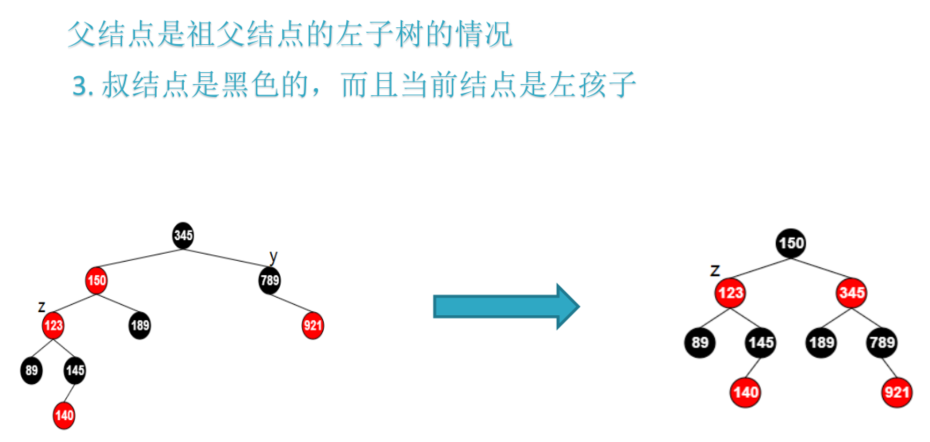
此时需要先将当前结点的父节点变为黑色，以及让爷结点变为红色，然后让爷结点进行一次右旋

void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
	// z是插入的结点，y是z的父节点，y是z的叔结点
    //只有当父节点是红的时需要调整，因为插入的节点必须为红，两个红色结点不能相邻
	while (z->parent->color == RED) { 
		if (z->parent == z->parent->parent->left) {
			rbtree_node *y = z->parent->parent->right;
			if (y->color == RED) { // 对应于CASE 1
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;
				// 回溯判断调整后是否满足红黑树条件
				z = z->parent->parent; // z --> RED
			} else {
				if (z == z->parent->right) {  // 对应于CASE 2
					z = z->parent;
					rbtree_left_rotate(T, z);
				}
				// 对应于CASE 3
				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_right_rotate(T, z->parent->parent);
			}
		} else { // 而对于父节点是爷结点右子树的情况，只需要镜像替换即可
             // left -> right, right -> left
			rbtree_node *y = z->parent->parent->left;
			if (y->color == RED) {
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;
				z = z->parent->parent; // z --> RED
			} else {
				if (z == z->parent->left) {
					z = z->parent;
					rbtree_right_rotate(T, z);
				}
				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_left_rotate(T, z->parent->parent);
			}
		}
	}
	T->root->color = BLACK;
}

红黑树插入结点

插入其实很简单，不过是判断大小找到合适的插入位置

void rbtree_insert(rbtree *T, rbtree_node *z) {
	rbtree_node *y = T->nil;
	rbtree_node *x = T->root;
	while (x != T->nil) {
		y = x;
		if (z->key < x->key) {
			x = x->left;
		} else if (z->key > x->key) {
			x = x->right;
		} else { //Exist
			return ;
		}
	}
	z->parent = y;
	if (y == T->nil) {
		T->root = z;
	} else if (z->key < y->key) {
		y->left = z;
	} else {
		y->right = z;
	}
	z->left = T->nil;
	z->right = T->nil;
	z->color = RED;
	rbtree_insert_fixup(T, z);
}

红黑树删除结点

待办

C++开发学习笔记